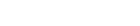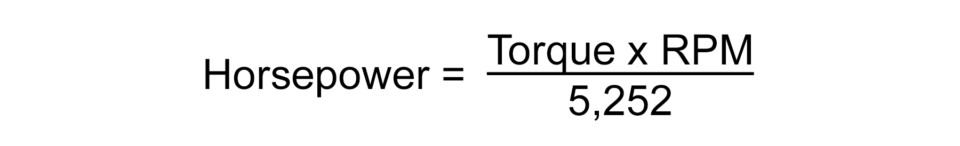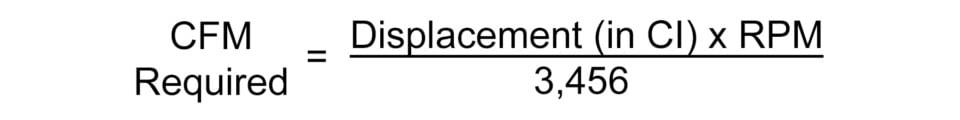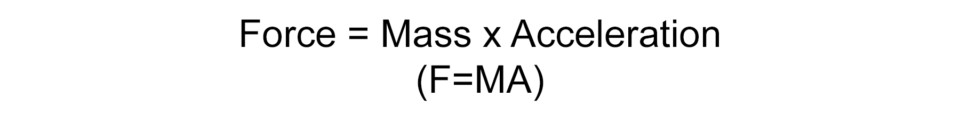There’s a whirling dervish of a physics lesson happening inside every engine, every time it spins at high RPM. The higher the revs, the more those dynamic forces play havoc with an engine. The one place where all this motion can thump you on the back of your head like an old schoolmarm is in the valvetrain. EFI University’s Ben Strader and Comp Cams’ preeminent cam designer Billy Godbold have collaborated on a project they call Spinal Tap. The goal is to spin an LS engine – reliably – to 11,000 rpm. Godbold and Strader are not abusing pushrods, valvesprings and rocker arms just for fun. This is all in the name of education.
Strader runs a school called EFI University in Lake Havasu City, Arizona where they teach not just EFI tuning, but also engine building and dynamics. Everything this pair has learned in this effort can be found in Starder’s Competition Engine Development (CED) class. Think of the class as an insider’s view into what it takes to build an NHRA Pro Stock engine. Spinal Tap will actually be part of an upcoming class project.
While the emphasis is on learning – it’s also about reliability. While hit-or-miss attempts might be able to stumble onto a combination that could achieve this lofty goal once, or maybe twice, it has taken Strader and Godbold’s concerted effort of well over a year of Spintron testing and applied physics to create the permutation of lobe design, lifter, pushrod, rocker arm, and valvespring that achieves this goal. True, the engine itself has yet to make noise, but EFI University and Comp Cams have invested the resources to perfect the combination. In testing, the valvetrain endured 30 consecutive simulated drag strip runs performed and measured on Comp’s Spintron machine, so reliability appears to be achievable. The real engine will be the ultimate test.
Spinning to the Moon
For those perhaps not familiar with a Spintron, it is the latest in engine testing technology developed and built by Trend Performance’s Bob Fox, to accurately measure what happens to the valvetrain at high engine speeds. The machine employs a 75-horsepower electric motor to spin a shaft that substitutes the crankshaft. This shaft drives a timing set in an actual RHS LS block housing a camshaft and the entire 16 lifters, pushrods, springs, intake and exhaust valves knobbing up and down against actual spring pressure on an RHS LS7 head. Lasers are used to track each valve to accurately measure within 0.002-inch of exact valve position. The system drives the entire valvetrain in order to simulate the torsional twist that tends to occur with camshafts working against high spring loads.
The Spinal Tap fight is kinetic energy vs. potential energy. – Ben Strader, EFI University
After multiple iterations, the result was a system that has proved capable of living quite comfortably at this rarified engine speed. That alone is impressive, but the physics involved with the system is worth investigating. The issues at play are just as real (if less pronounced) at 7,000 rpm as they are at 11,000 rpm, so the data is certainly worth studying even if you never aspire to five-digit engine speeds.

This is one of the three Spintron machines that Comp Cams has acquired in search of knowledge regarding high-RPM valvetrain stability. A 75 horsepower electric motor spins a shaft that drives the cam gear mounted in the engine block. The system actuates all 16 valves for the engine, which is why it needs a such a powerful motor.
Before we get into the heavy lifting, it is worth examining how horsepower is calculated and why we would want to spin engines to the extreme. The whole point of building an engine to spin faster is predicated on a simple equation first created by the Scotsman James Watt who came up with a calculation for horsepower. All engines make torque, but that is only a measurement of twisting force. Work is defined as that torque over a period of time. Completing one step an hour up a staircase is work, just not nearly as much compared to charging up three stories of stairs in 30 seconds.
The same is true with engines. In this application, time is represented as revolutions per minute (RPM). Watt’s equation simplifies down to:
There’s quite a bit to this simple math puzzle by observing that the denominator (the number below the division line – 5,252) is a constant. So even if we maintain the torque, by making the RPM numerator larger (higher RPM), this means we are performing the same twisting effort over a shorter period of time and as a result, the engine will make more horsepower. It’s that simple.
As an example, if an engine makes 400 lb-ft of torque at 5,252 rpm, we can see that this will result in making exactly 400 hp because the numerator and denominator are equal values. If we make 400 lb-ft at 5,000 rpm, the formula tells us the engine will make 380.8 horsepower. However, if we design an engine to reliably make the same 400 lb-ft at 10,000 rpm, common sense tells us that we have performed the same work in half the time. This doubles the result: 380.8 x 2 = 761.6 horsepower. If we then push this 400 lb-ft to 11,000 rpm, this will net 837.8 horsepower. All of that elegance is found in a simple equation.

Because there are no pistons in the engine, the block is cut to allow placing a laser beam sensor to measure valve position. According to Godbold, the system is accurate to 0.002-inch of valve height. This is the device which creates the precision data graphs.
It’s More Than Just Revs
But additional RPM isn’t a guarantee of horsepower. We also need airflow. So let’s look at a simple equation that Strader offers in his CED course. This is a way of estimating the volume of air (in cubic feet per minute) the engine will need at that engine speed to make peak power. This is just an estimate but it points us in the right direction.
Let’s use the example of a 6.2L 376ci engine at 5,000 rpm:
This means the engine will require 544 cfm air to make peak power at this RPM. If we double the engine speed to 10,000 rpm, this tells us the engine will demand 1,088 cfm. But as Strader explains, “That assumes the intake valve is open 100-percent of the time, which it is not. With Spinal Tap’s cam specs at 288 degrees at 0.050, we can express this as a percentage.”

These are the pushrods used in the Spinal Tap Spintron tests. The intake pushrod girth measures 1/2-inch that tapers to 7/16-inch and weighs a hefty 167 grams. The exhaust pushrods are even heavier, tapering from 9/16-inch to 7/16-inch and weigh in at 188 grams. That’s a 5/16-inch pushrod on the bottom for comparison. In the north country, those monster pushrods would require an “ooof-dah.”
Strader quickly explained that if we take 288 degrees of valve open time divided by 720 degrees (two revolutions for a complete the four stroke cycle), that equals 40-percent (288 / 720 = 0.40). So now 1,088 cfm divided by 0.40 gives us 2,720 cfm. Divide that number by eight intake ports and the flow becomes 340 cfm, which is a great estimate of the intake port flow necessary to make the expected power. There’s a whole story in these two paragraphs because we took several shortcuts that deserve more explanation in order to explain this briefly. We can go into more detail on this at a later date.
Now that we know the amount of air we’re moving, Strader’s CED class offers yet another formula for estimating horsepower for naturally aspirated engines. The first step is determining torque potential by multiplying displacement times 1.5 lb-ft of torque per cubic inch (lb-ft/ci). This 1.5 lb-ft/ci number is aimed at really good competition engines. For milder street engines, you can substitute 1.25 lb-ft/ci or perhaps a number in between.
This 1.5 lb-ft/ci equals the engine’s max torque number. Next, Strader has observed that most competition engines lose roughly 12-percent of that torque at peak horsepower, so we take that peak torque and multiply it by 0.88. The final step is to choose the RPM point for peak power (based on cam timing and cylinder head flow) and finish the formula.
Here’s an example using the same 376ci LS engine:
TQ = 376 x 1.5 = 564 lb-ft of torque
Peak TQ x 0.88 = 496 lb-ft at peak-horsepower RPM
Peak RPM estimate = 6,300
This final step is merely executing the classic HP equation TQ x RPM / 5252:
You may notice that if all we do is bump up the peak horsepower RPM point, the horsepower number will always be larger. That is true. But keep in mind that raising the RPM level involves delivering more air, along with a tremendous amount of effort, skill, and money to build an engine that will spin to that elevated RPM – and live!
So clearly RPM comes at a price. In the very early days of racing, engine builders discovered that RPM took a heavy toll on engine components – especially valvetrain pieces. But In the intervening millennium, technology has radically improved and now materials like titanium valves and NASA-quality valvesprings will happily do the job – at a price.

This is the valvespring that controls all that chaotic valve action. It is a PSI dual spring that can accommodate over a 1.00-inch valve lift with an open load of 1,230 pounds.
From Theory to Practice
Before we get into the actual Spintron trace data, let’s set the stage for what is on the test stand. With the RHS block and heads in place, the Comp mechanical roller cam uses a brand new lobe that Godbold designed multiple variations of, specifically for this effort. The specs may seem conservative with 288 and 308 degrees at 0.050 duration and a theoretical lift number of 1.045-inch on the intake. The lobes were placed on a much larger 60mm core actuating a Jesel 0.937-inch diameter lifter with a 0.975-inch diameter wheel. This produces what is called a wheel-guided lifter that we covered in the first Spinal Tap story.
The Jesel rocker ratio is 1.9:1 and leverages against a PSI valvespring with 410 pounds on the seat and 1,200 pounds open. If you multiply 1,200 pounds times a rocker ratio of 1.9:1, the pushrod is working against almost 2,300 pounds of load; those are some brutal loads – and that’s before the dynamics begin their evil sorcery.
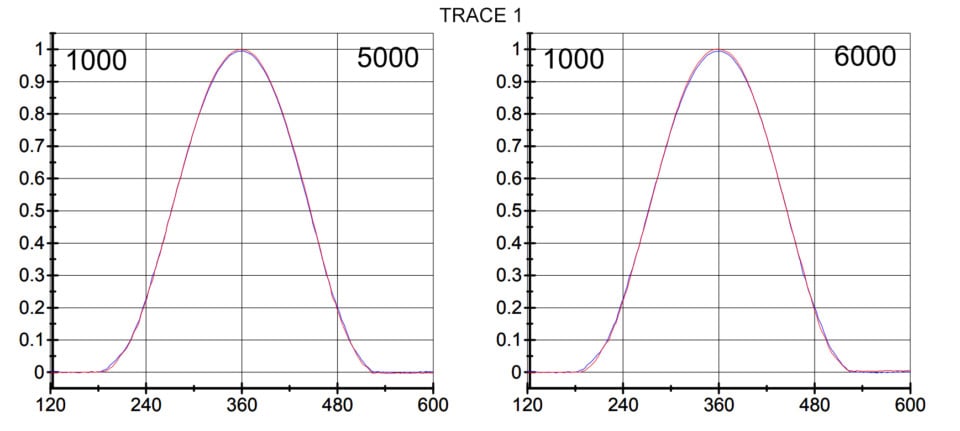
When accelerating valvetrain components at high-RPM, these forces tend to deflect components like pushrods to a much greater extent than can be simulated with a static dial indicator measurement. At speed, the energy put into the pushrod that causes the deflection is eventually released back into the system and that can create problems. Godbold sent us a valve lift trace from a later Spinal Tap Spintron test in which the accompanying graphs show the blue as the valve lift curve with the engine running at 3,000 rpm while the red trace reveals the valve positions (and deflection) at various engine speeds right up to 11,200 rpm.
We’ll first take a look at Trace 1 where the spring is in complete control of the valve. This was from the Spinal Tap engine running at 5,000 and 6,000 rpm. Beginning on the left side of the graphs on Trace 1, the red line reveals a small amount of deflection (which is a loss of lift) just as the valve accelerates off the seat. As the system bends, this reduces the area compared to the blue lift curve. If you look carefully on the 6,000 rpm graph on the right, you’ll see a tiny amount of increased lift where the red curve shows greater lift just after the peak. This is where there is less deflection compared to the load at 1,000 rpm so this is the reason for the slight addition to lift. All of this deflection is considered normal and is not going to cause any serious damage to the valvetrain.
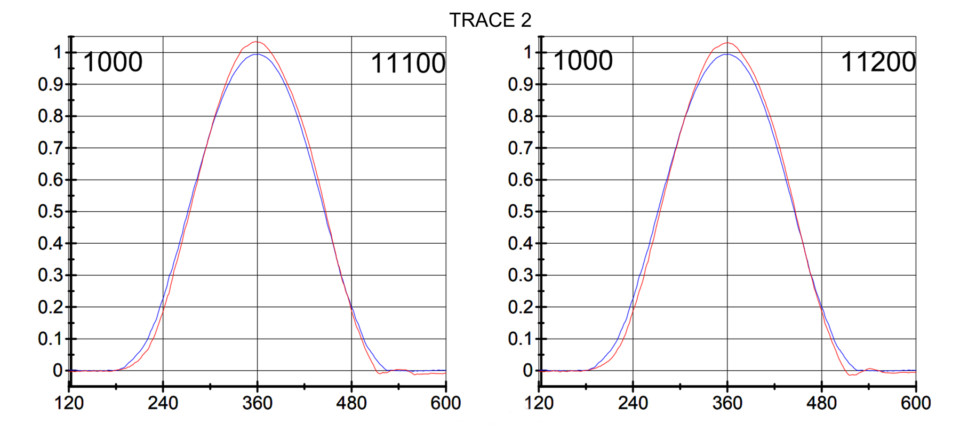
Moving to Trace 2, this is the exact same combination now spinning at 11,100 and 11,200 rpm. This is nearly double the RPM from Trace 1. Note there is more deflection at the opening point with a greater amount of separation just past peak lift, followed by the closing side where it really gets dramatic.
There is significant valve loft in this situation occurring before the peak in the 1,000-rpm red trace curve. This is where the energy stored in the pushrod deflection is released and it adds this lift at the point where the valve should be slowing at peak lift. This lofts the valve beyond the baseline lift, creating valvetrain separation within the system and does not return to the baseline curve until roughly 0.400-inch of valve lift on the closing side.
Note what happens after the valve closes. There is sufficient energy stored in the spring when the valve slammed closed to leverage against seat load to force the valve to bounce off the seat for a short period of time. Godbold considers anything under 0.015-inch as a mild bounce that would not show up in O2 sensor readings or in power. This can be considered “under control” but is significant as the beginning of what is commonly called valve float, where the power drops like falling off a cliff. A more accurate description of valve float would be “loss of control.”

After a series of tests are performed on the Spintron, a quick check of seat load will indicate if the spring is suffering from duress and may soon fail. This is the same kind of test you see the Pro Stock racers performing in the pits between rounds.
Maintaining Control At All Costs
The position on the graphs where the red trace loses lift compared to the blue line is where the valvetrain is bending as a result of the acceleration forces. These forces are massive. This is where Godbold gets a grin on his face and lets fly with some basic physics. He always starts with the classic:
This describes exactly what is happening in the valvetrain. With a given amount of mass in the valvetrain, when acceleration is applied by the cam lobe at a given RPM – force is the result. That force is applied to the valvespring. The spring’s job is to control both the static and inertial forces and not allow them to overcome the system. If the spring is conquered by a greater force, loss of control is the result.
Godbold’s other favorite formula explains why higher engine speeds make controlling the valvetrain so difficult. This is the definition of kinetic energy that again involves the mass of components joined with thier velocity:
This formula divides the mass in half (1/2m) but also squares the velocity (v2). So if we double engine speed from 5,500 to 11,000 rpm, the velocity-squared portion of that formula quadruples the force. Ideally, the valvesprings must be stronger and the entire valvetrain must be incredibly stiff in order to control the forces that are inherent with increased engine speed.
Stated another way, the potential energy of the load stored in the compressed valvespring must be greater at any useful engine speed than the kinetic energy applied to the system by the cam lobe. This includes the g-forces created when mass is accelerated (F=MA). If you can embrace the physics, it can make working with high-RPM engines a little easier to understand.
According to Godbold, it’s not unusual for a small-block Chevy to experience a g-force load at valve opening or closing of 1,500g. If we use a small-block pushrod that weighs 115 grams, when subjected to a force of 1,500g that pushrod instantaneously weighs 172,500 grams – which is 380 pounds!
The ‘velocity-squared’ part of that equation is what gets you. – Ben Strader, EFI University
The exhaust pushrod used in the Spinal Tap engine is a massive 9/16-inch diameter unit and larger than the intake pushrod because the exhaust side is opening against residual cylinder pressure and therefore sees a greater load. This pushrod is 8.550-inches long and weighs 188 grams. If we use a 3,000 g-force number for this engine (it actually is much higher), this conservative number still represents 1,240 pounds of force generated by each exhaust pushrod!
All of these forces directly affect how the valvetrain responds to elevated engine speeds. There are several possible solutions, but the stiffer the system, the more reliable it becomes. A stiffer system does a better job of controlling the dynamic accelerations closer to the theoretical 800-1,200g instead of the more abrupt 2,000g-4,000g numbers.

Early testing resulted in damage to the valvespring end tips, which were bouncing off either the spring seat or against the valvespring retainer. This is a great indicator of valve distress and called for changes to the system – mainly an increase in spring load and changes to the lobe acceleration forces.
As a way of testing a given valvetrain’s stiffness, Godbold suggests first measuring the system’s theoretical maximum lift using a light duty checking spring and a dial indicator on the valve retainer. Then repeat this max-lift test but with the actual intended valvespring, as we covered in this article on valvetrain stiffness. In nearly every case, there will be a loss of peak valve lift.
He then recommends dividing the peak lift spring load by the amount of deflection as a way to evaluate the system’s overall stiffness. In the case of the Spinal Tap valvetrain, Strader measured a maximum lift deflection of 0.046-inch at a peak spring load of 1,230 pounds. Doing the math produces a value of 26,739 lbs/inch as a stiffness factor. We’ve taken to calling this number the Godbold Stiffness Rating – or GSR – which should not be confused with the other “GSR”s of Gun Shot Residue or Galvanic Skin Response – which is the process used in lie detector testing.

They say you can’t tell a book by its cover – or in this case the quality of the springs by the box. These PSI dual springs for the Spinal Tap valvetrain may come in a modest container, but they did a superb job on the Spinal Tap engine.
For competition high-RPM engines, Godbold says the minimum GSR is 20,000 lbs/in, but he prefers to see it above 25,000 lbs/in. The Spinal Tap engine tested over 26,000 lbs/in, reinforcing the point that the valvetrain is suitably stiff. If you truly aspire to greatness, Godbold says the Pro Stock and NASCAR guys operate in the 30,000 lbs/in arena. Another point worth mentioning is this GSR number is intended for competition engines with very high spring loads and the rating system is aimed at these applications. It is not linear, meaning that with lighter springs and less deflection as seen on street engines, the GSR numbers will be higher, but that does not necessarily indicate a genuinely stiffer system.
There’s much more to the testing on Spinal Tap but this story has already flapped its wings way too long. There’s another full story just on the abuse heaped on valvesprings at elevated RPM levels. Perhaps we’ll save that one for a later date if enough tech-heads would be willing to accompany us down that particular rabbit hole. Let us know in the comments section.
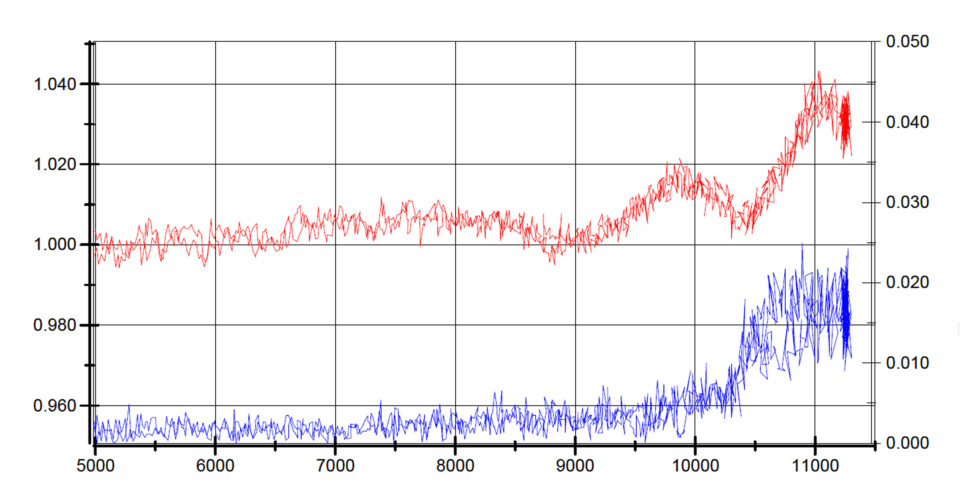
This may look like a seismograph trace of California falling off into the Pacific – but it’s really another way to look at one of the final Spinal Tap Spintron tests. The vertical (Y) axis on the left is actual valve lift that is displayed on the blue line. The red line is the amount of valve lift deflection that is called out on the right Y axis. Engine speed (RPM) is noted along the horizontal (X) axis. Note that valve lift remains relatively stable from 5,000 to 10,000 rpm and then begins to both increase and fluctuate more wildly above 10,000 rpm. This increase in lift is valve loft of roughly 0.040-inch. Note that the red curve (deflection) is relatively stable until 9,000 and then increases slightly at 9,700 rpm, subsequently drops and then spikes dramatically at 11,000. The inertial forces present at 11,000 rpm and beyond are so great that the system loses control around 11,300 rpm where the test was terminated. This test also revealed that dynamically, the maximum valve lift deflection was just slightly more than 0.045-inch, which is an excellent number given the spring load.

This is Ben Strader, president and owner of EFI University and the driving force and co-conspirator behind the Spinal Tap effort.